ConnAttractor

`connattractor`¶

for Connectivity-based Hopfield Neural Networks (CHNNs)

Installation¶

pip install connattractor

Hint

The package is to be considered a “low-key research preview”. Compatibility with various versions of the dependencies is not fully guaranteed. To run analyses in a fully reproducible way, use the docker container:

install docker

clone the repo and start your notebook in a docker container

git clone https://github.com/pni-lab/connattractor.git
cd connattractor
docker run -it -v $PWD:/mounted/connattractor -p 8080:8080 -p 8888:8888 pnilab/connattractor:latest jupyter notebook

copy paste the last link in your browser to start the notebook

QuickStart Guide¶

Contents¶

Part 1: The quickest way to plot and analyze your data on the CHNN projection
Part 2: Build your own CHNN projection

Imports

import sys
sys.path.append('..')
import pickle
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from connattractor import network, analysis, utils

Part 1: The quickest way to plot and analyze your data on the CHNN projection¶

For the quickest start, you can load the pre-computed embedding, calculated on the example connectome provided with the package.

hopfield_embedding = utils.get_fcHNN_template_embedding()

Load the example task data (scrubbed and seperated into task and rest)¶

rest, sub_rest, task, sub_task = utils.get_ex_task_data()

perc. scrubbed: 0.8133971291866029
perc. scrubbed: 0.5741626794258373
perc. scrubbed: 0.6267942583732058
perc. scrubbed: 0.7081339712918661

((405, 122), (1052, 122), array([42.3, 43.3, 44.3, 45.3, 46. , 46.3]), 405)

Plot the data in the projection plane¶

To get a good impression on the data in the projection, we first plot a contourplot of all activations of the rest data and plot the mean activations during rest of all study participants on the projection. We repeat the same for the task data.

fig, ax = plt.subplots(1, 2, subplot_kw={'projection': 'polar'}, figsize=(8, 4))
    
hopfield_embedding.plot(rest, plot_type='contourf', ax=ax[0],
                    density_bins=30, density_sigma=1, levels=6, alpha=0.8, cmap='Blues',
                    attractor_plot_type='glassbrain', attractor_kwargs=dict(cmap='binary'),
                    regimes_fill_kwargs=dict(alpha=0.0),
                    regimes_contour_kwargs=dict(alpha=1.0, colors='black')
                   )

sub_means_rest = np.array([np.mean(rest[sub_rest==sub], axis=0) for sub in np.unique(sub_rest)])
sub_means_task = np.array([np.mean(task[sub_task==sub], axis=0) for sub in np.unique(sub_task)])

hopfield_embedding.plot(sub_means_rest, plot_type='scatter', ax=ax[0],
                        marker='^', c='black', s=30,
                        attractor_plot_type='scatter', attractor_kwargs=dict(alpha=0),
                        regimes_fill_kwargs=dict(alpha=0.0),
                        regimes_contour_kwargs=dict(alpha=1.0, colors='black')
                       )
ax[0].set_yticks([])
ax[0].grid(False)


hopfield_embedding.plot(task, plot_type='contourf', ax=ax[1],
                    density_bins=30, density_sigma=1, levels=6, alpha=0.8, cmap='Reds',
                    attractor_plot_type='glassbrain', attractor_kwargs=dict(cmap='binary'),
                    regimes_fill_kwargs=dict(alpha=0.0),
                    regimes_contour_kwargs=dict(alpha=1.0, colors='black')
                   )

hopfield_embedding.plot(sub_means_task, plot_type='scatter', ax=ax[1],
                        marker='^', c='black', s=30,
                        attractor_plot_type='scatter', attractor_kwargs=dict(alpha=0),
                        regimes_fill_kwargs=dict(alpha=0.0),
                        regimes_contour_kwargs=dict(alpha=1.0, colors='black')
                       )


    

ax[1].set_yticks([])
ax[1].grid(False)
plt.show()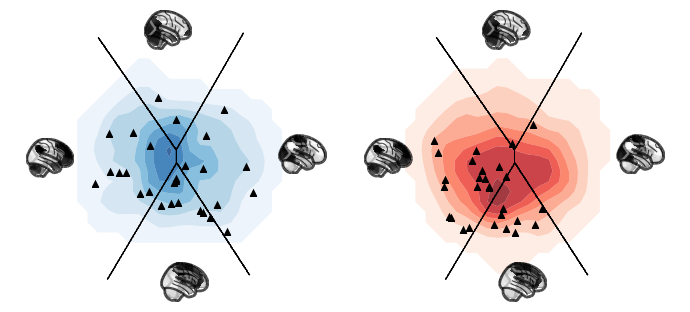

Statistical analysis¶

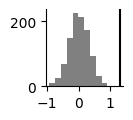
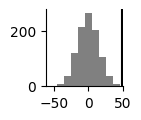
To compare the two conditions statistically with a permutation test, compare the position difference in the projection plane as well as the absolute energy difference as test statistics. In this example we calculate 1000 permutations, swapping the conditions and plot the actual difference against the null distribution.

from numpy.linalg import norm
random = np.random.default_rng(42)
noise = 0.37
num_perm = 1000


sub_means_rest = np.array([np.mean(rest[sub_rest==sub], axis=0) for sub in np.unique(sub_rest)])
sub_means_task = np.array([np.mean(task[sub_task==sub], axis=0) for sub in np.unique(sub_task)])

task_embedded = hopfield_embedding.embedding_model.transform(sub_means_task)[:, :2]
rest_embedded = hopfield_embedding.embedding_model.transform(sub_means_rest)[:, :2]
diffs = task_embedded - rest_embedded
true_diffs_norm = np.array([norm(d) for d in diffs])
true_diff_mean = np.mean(true_diffs_norm)

energy_rest = np.array([hopfield_embedding.hopnet.energy(s) for s in sub_means_rest])
energy_task = np.array([hopfield_embedding.hopnet.energy(s) for s in sub_means_task])

true_energy_diff = energy_rest - energy_task
true_energy_diff_mean = np.mean(true_energy_diff)

n = len(diffs)
diffs = []
energy_diffs = []

for p in range(num_perm):
    # swap conditions randomly (i.e. sign flip)
    
    perm_i = random.choice([1,-1], n)
    diffs.append(np.mean(true_diffs_norm * perm_i))
    energy_diffs.append(np.mean(true_energy_diff * perm_i))


plt.figure(figsize=(1,1))
plt.hist(diffs, color='gray')
plt.axvline(true_diff_mean, color='black')

plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.show()

plt.figure(figsize=(1,1))
plt.hist(energy_diffs, color='gray')
plt.axvline(true_energy_diff_mean, color='black')

plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.show()


print('p(projection) =', (diffs>true_diff_mean).sum()/num_perm)
print('p(energy) =', (energy_diffs>true_energy_diff_mean).sum()/num_perm)

p(projection) = 0.0
p(energy) = 0.0

Part 2: Build your own CHNN projection¶

Obtain functional connectivity matrix¶

Should be a partial correlation matrix, square and symmetric.

Below, we load in an example connectome, derived from study 1 of the manuscript. Given the high replicability and generalizability of CHNN analyses, the connectome does not have to stem from the analyzed dataset. Similarly to anatomical standrad templates in neuroimaging practice, the supplied example connectome can be considered a standard connectome template.

Users are, nevertheless, encouraged to use dataset-specific connectomes.

Let’s load in the example connectome¶

mtx = utils.get_ex_connectome()
mtx

Construct your fcHNN¶

hopnet = network.Hopfield(mtx)
hopnet.plot_weights()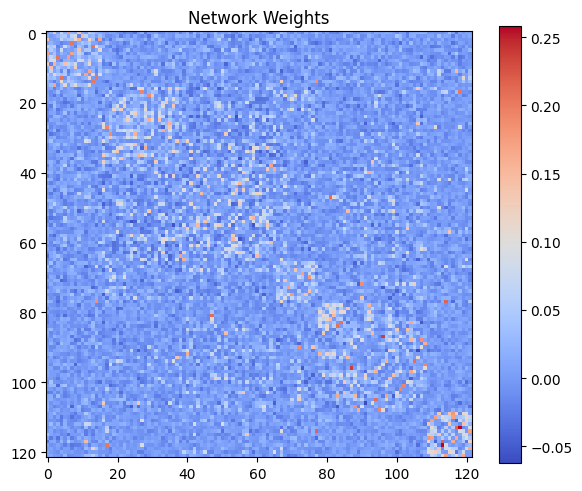

Run the stochastic relaxation procedure to obtain simulated states¶

It may take a few seconds...

chnn_state_space = analysis.simulate_activations(mtx.values,
                                            noise_coef=0.37,
                                            num_iter=100000,
                                            beta=0.04,
                                            random_state=42)

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 100000/100000 [00:21<00:00, 4619.54it/s]

Create your Hopfield Embedding¶

Again, a few seconds...

chnn_projection = analysis.create_embeddings(chnn_state_space,
                                             attractor_sample=1000,
                                             random_state=42)

100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 1000/1000 [00:59<00:00, 16.92it/s]

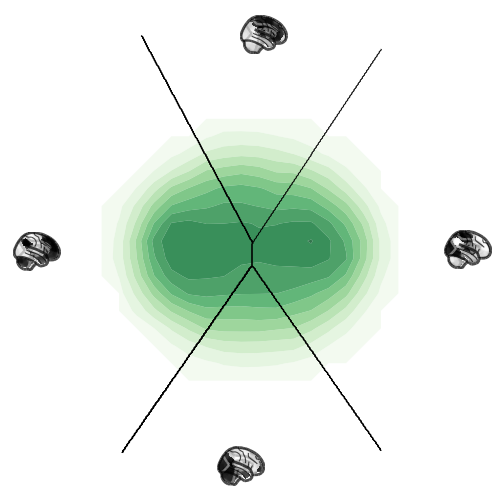
Plot the state space¶

ax = chnn_projection.plot(chnn_state_space.states, plot_type='contourf',
                          density_bins=30, density_sigma=0.5, levels=12, alpha=0.8, cmap='Greens',
                          attractor_plot_type='glassbrain', attractor_kwargs=dict(cmap='binary'),
                          regimes_fill_kwargs=dict(alpha=0.0),
                          regimes_contour_kwargs=dict(alpha=1.0, colors='black')
                         )
ax.set_yticks([])
ax.grid(False)