Abstract¶
Information processing in the brain is both distributed across multiple regions and hierarchical in nature. Higher-order cognitive functions, complex emotions, and multifaceted experiences such as anxiety, fear, pain, or self-awareness are believed to be represented and governed by higher-order “integrator regions” at the top of this hierarchy, which have access to all information relevant to these complex processes. However, these very functions often resist empirical mapping to any single brain region. Here, we introduce a theoretical framework in which large-scale integrative information processing at the apex of the computational hierarchy is achieved through the attractor dynamics of the entire system, rather than through dedicated integrator regions. We present a prototypical mathematical formalization of this concept, which involves marginalizing a hierarchy of free-energy-minimizing integrator nodes into an equivalent recurrent network composed solely of lower-level units. In this network, higher-level units manifest as attractor states. Our framework elucidates the computational mechanisms underlying the active inference processes that drive attractor dynamics and establishes connections to Bayesian causal inference, predictive coding, and computational emergence within the brain. We propose and demonstrate practical methods for reconstructing these dynamics from empirical data, discuss existing evidence that supports this theory and explore its implications across various fields, including the formulation of testable hypotheses and predictions.
Introduction¶
Complex cognitive processes, experiences, and emotions such as happiness, sadness, anxiety, fear, pain, or self-awareness share a common characteristic: they all require comprehensive integration of information from numerous sources. This includes perceived features of the world (processed through complex sensory chains), our own physiological and cognitive states, action-readiness, long-term reactive dispositions, as well as short-term, long-term and autobiographical memories and contextual information. For instance, the experience of pain arises from processes far more intricate than a mere feedforward evaluation of sensory and nociceptive inputs. Actual pain experiences integrate and interact with emotional and cognitive states, expectations, memories, and contextual information. Pain can even emerge in the absence of an external painful stimulus, as seen in various types of chronic pain. If such high-level functioning relies on internal self-monitoring of a vast array of the brain’s states, it is reasonable to hypothesize that the resulting subjective experiences are represented and generated by hub-like regions at the top of the brain’s computational hierarchy. These hubs are interconnected with all relevant modules to access the necessary information effectively. However, these very complex and subjective functions resist empirical mapping to any single brain center.
There are several complementary and competing theories regarding how integrative processing occurs and how it gives rise to subjective experiences. These include hierarchical (Bayesian) causal inference Körding et al., 2007Shams & Beierholm, 2022, hierarchical predictive coding Rao & Ballard, 1999Hohwy, 2013, global (neuronal) workspace theory Tononi, 1998, the “inner screen model” Ramstead et al., 2023, and the Hierarchically Mechanistic Mind (HMM) framework Badcock et al., 2019. Most of these theories propose the existence of an essential, irreducible subsystem that has access to all relevant sources of information within the brain to infer those complex characteristics of the external world that cannot be directly measured, but are decisive for the given experience or behavior. To have access to a broad pool of information, this subsystem must be situated at the top level of the computational hierarchy. It is envisioned as a complex “meta-controller” that formulates and implements the best guess about the deep causes of all incoming inputs. There is however a fundamental disagreement about where such top-level integrator hubs (or “innermost screens”) could be located. For instance, in the framework of predictive coding, such integrative functioning is often attributed to higher order cortical areas, such as the prefrontal cortex or the parietal and temporal association areas. Similarly, proponents of the global workspace theory identify the integrative global workspace as a network of excitatory neurons connecting the prefrontal and parietal cortices Mashour et al. (2020). In contrast to cortico-centric theories, theories like felt uncertainty theory Solms, 2019 postulate the brainstem as the pinnacle of hierarchical organization, whereas the inner screen theory is exemplified with the hippocampus as a potential candidate for an “innermost screen” of information integration Ramstead et al., 2023.
One of the most promising candidates for such integrative computations is not a specific physical brain region but rather the complex dynamics that arise from the interactions of multiple regions. These network dynamics can organize around multiple stable states, known as attractor states. Attractor dynamics have long been proposed to play a significant role in information integration at the circuit level (Freeman (1987); Amit (1989); Tsodyks (1999); Deco & Rolls (2003)) and have become established models for canonical brain circuits involved in motor control, sensory amplification, motion integration, evidence integration, memory, decision-making, and spatial navigation (see Khona & Fiete (2022) for a review). Multi- and metastable attractor dynamics have also been proposed to extend to the meso- and macro-scales Rolls, 2009, “accommodating the coordination of heterogeneous elements” Kelso, 2012. Thus, such dynamics play a critical role in modeling meso- and macro-scale brain functions by integrating mean-field and neural mass models with dynamical systems theory and coordination dynamics Haken, 1978Breakspear, 2017Deco & Jirsa, 2012Kelso, 2012.
Here, we present a prototypical mathematical formalization that illuminates the mechanisms by which attractor dynamics facilitate information integration. Furthermore, we propose a novel conceptual framework wherein high-level integrative computations, such as causal inference, are executed by the large-scale attractor dynamics of the entire system rather than through dedicated physical hub regions.
Our approach benefits from the statistical equivalence between attractor states in recurrent networks and top-level hub nodes in hierarchically organized multi-layer networks. In the recurrent system, higher-level integrator nodes no longer possess a physical existence; instead, they manifest as attractor states of the system. Nonetheless, their influence on lower-level nodes remains unchanged. We demonstrate that, in such systems, active inference (through free energy minimization Friston et al. (2009)) at the global system level emerges from active inference within distinct neural units. These computations require broad and comprehensive integration of the brain’s internal states, which arise as emergent processes implemented by the attractor dynamics of the entire recurrent network. This approach eliminates the necessity for actual physical top-level hub regions, offering a less vulnerable and more economical solution compared to the reliance on explicit physical integrative hub regions. We explore several implications of the proposed mathematical formalization, including its relationship to Bayesian causal inference and predictive coding. Additionally, we provide computational and analytical methods for reconstructing attractor states from empirical data and emphasize the emergent nature of computations performed by attractors. Finally, we present initial evidence supporting the proposed framework, discuss the underlying assumptions, and examine its applications and implications across various research fields. We conclude by proposing testable hypotheses and predictions that arise from the framework.
Results¶
Active Inference and Information Integration¶
Our formalization starts from the Free Energy Principle (FEP) Friston et al., 2009Friston, 2010Friston et al., 2023, which is arguably the most general and widely applied framework for explaining the structure, function, and dynamics of the human brain Friston et al., 2009Parr et al., 2022Friston et al., 2016Pezzulo et al., 2024. The core concept is that any persistent dynamical system (e.g. ourselves, our brain, its regions or a single neuron) must maintain conditional independence from its environment by establishing a boundary, or statistically, a Markov blanket. Consistently maintaining the Markov blanket is equivalent to an inference process in which internal states infer external states through the blanket states (i.e., sensory and active states) by minimizing variational free energy (Figure 1A; Friston et al., 2009Friston, 2010Friston et al., 2023).
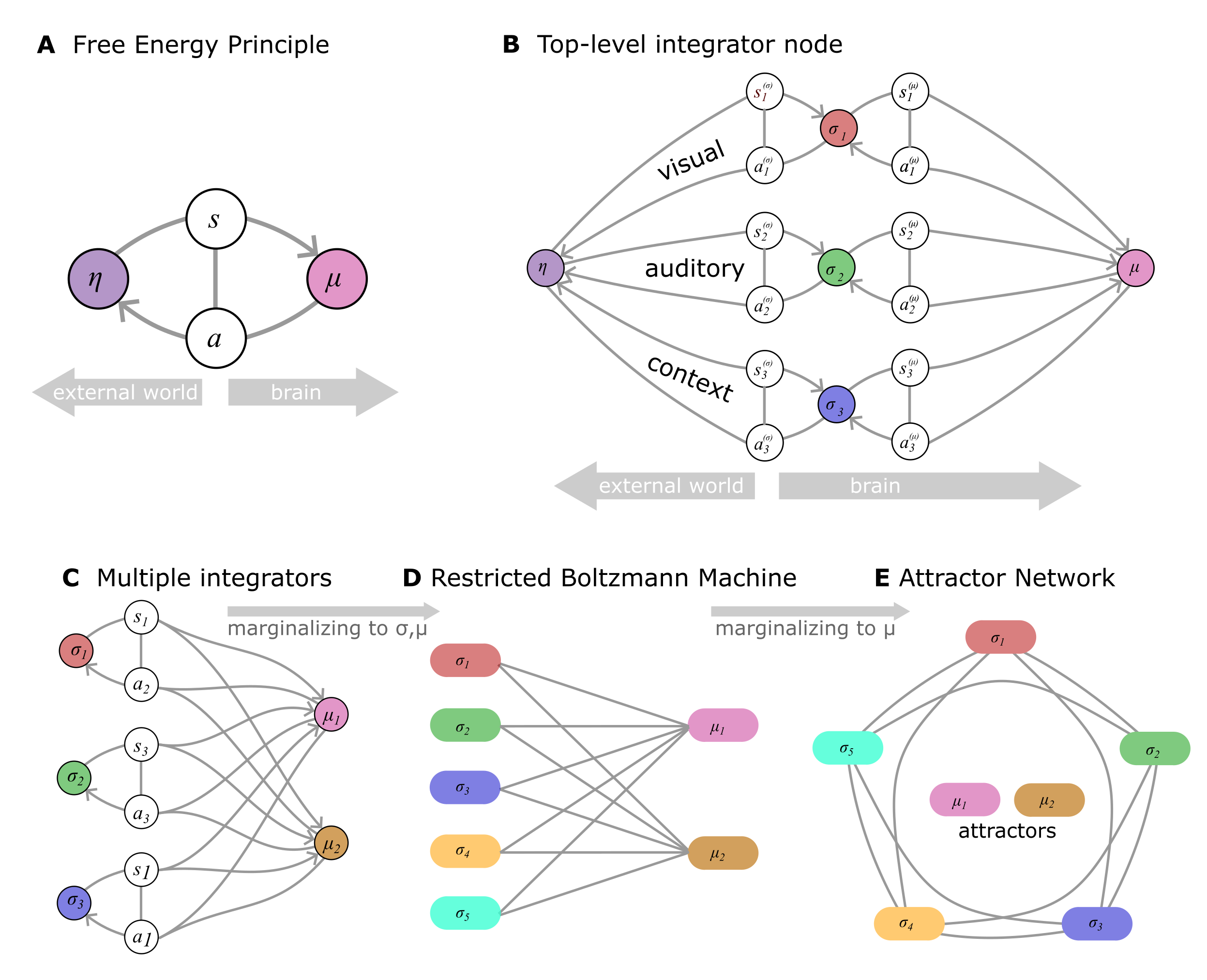
Figure 1:From the Free Energy Principle to Top-Level Information Integration via Attractor Dynamics.
A Schematic illustrating the division of a system into internal states (μ) and external (hidden, latent) states (η), separated by a Markov blanket consisting of sensory states () and active states (). The internal and sensory states minimize a free energy functional of the sensory inputs. The resulting self-organization of internal states corresponds to perception, while actions link the internal states back to the external states.
B Typically, the external state (η) cannot be directly observed, and only certain features (e.g., color, shape, sound) can be measured. In such cases, information about these distinct features is conveyed through different channels and inferred by separate “low-level” internal states (). These low-level internal states are then processed by a higher-level integrator state (μ), which conducts active inference on the , thereby indirectly inferring the latent external state (η) by minimizing free energy.
C Various aspects of the external state, or distinct external state variables, can be inferred by adding more integrator nodes. Each integrator node conducts active inference on multiple (or all) lower-level nodes simultaneously.
D In this paper, we demonstrate that, under a specific parametrization, this architecture is statistically equivalent to a Restricted Boltzmann Machine (RBM).
E The RBM can be marginalized into a stochastic recurrent network (a stochastic continuous-state Hopfield network in our prototypical parametrization), wherein the higher-level integrator nodes become attractor states of the system.
The equivalence between RBMs and attractor networks allows us to draw parallels between integrative computations performed by attractor dynamics and active inference (and Bayesian Causal Inference) as implemented by conventional hierarchical architectures.
This forms the basis of our conceptual framework, wherein top-level information integration is achieved through the attractor dynamics of the entire system, rather than via explicit physical integrator nodes.
The Free Energy Principle (FEP) can be formulated and parametrized in various ways. For example, the internal states of a neuronal subsystem at any scale may encode expectations or predictions about input signals received from other subsystems. These predictions are transmitted downward to lower hierarchical levels as actions. Conversely, the outputs from these lower levels, which represent prediction errors within this specific formulation, are sent back to the neural subsystem’s sensory states. This feedback allows the subsystem to update its predictions accordingly, a process known as (hierarchical) predictive coding Friston et al., 2012Hohwy, 2020Lee & Mumford, 2003Mumford, 1992Rao & Ballard, 1999. At the highest level, all FEP-based models concur that integrative processing in the brain entails the ability to combine and provide feedback on information from multiple sources (). This integration generates a coherent representation (μ) of an arbitrary latent external state (η) (Figure 1B), which is not directly observable and can only be measured through a few indirect aspects or features. As an example, we can consider that the external state-of-interest is (the probability of) physical tissue damage, and the corresponding internal state is pain. In this case relevant information sources will not only include sensory channels (primarily nociception, but also visual, auditory, or even olfactory cues, as interpreted by low-level brain regions), but also information coming from internal brain states, including emotional and cognitive states, expectations, memories, and contextual factors (e.g., attentional analgesia, placebo effects, and other forms of pain modulation). Some of these sources are more informative for inferring tissue damage than others. Consequently, the integrator unit responsible for inferring tissue damage must connect to all relevant brain areas and appropriately weigh the information from these diverse sources.
Parametrization¶
To provide a prototypical mathematical formalization of the concept, we employ the parametrization illustrated in Figure 2.
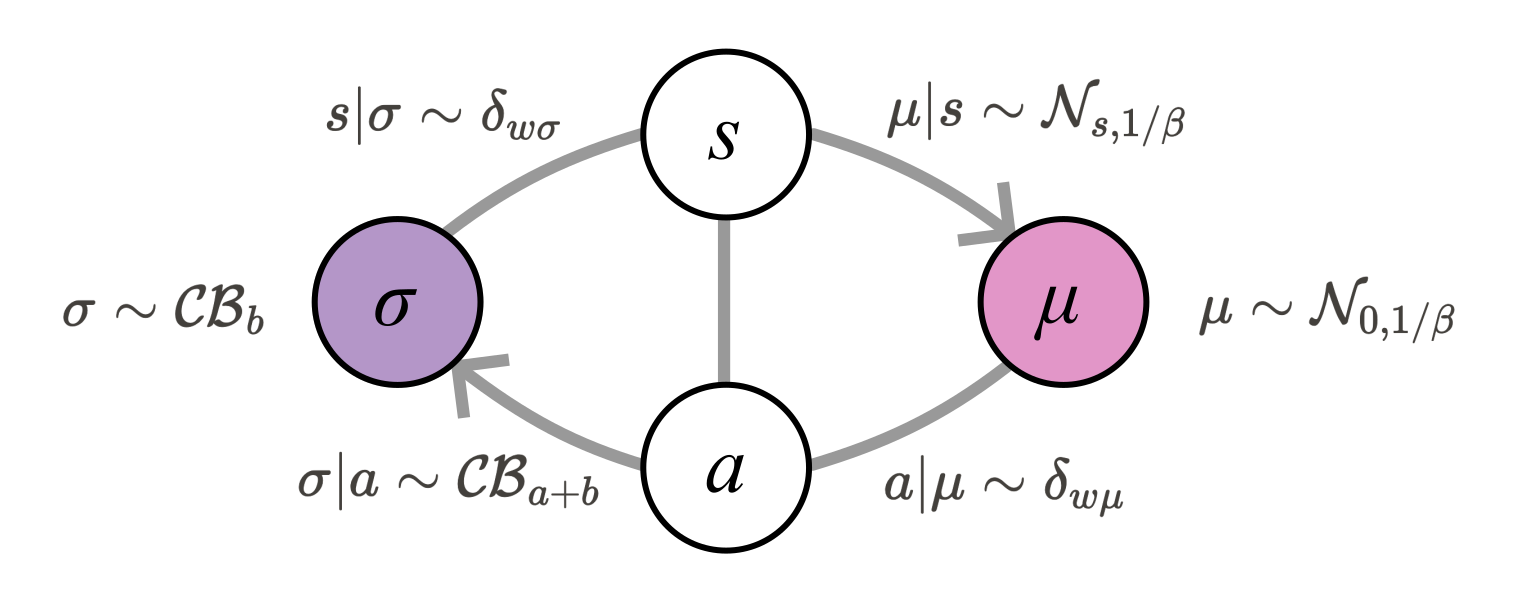
Figure 2:A Single Free Energy-Minimizing Unit with Our Parametrization.
The unit comprises a lower-level state (), both an active () and a sensory state (), and an integrator state (). The sensory state’s prior is modeled as a restricted continuous Bernoulli distribution with a prior bias () Supplementary Information 1. The integrator state follows a Gaussian distribution with a precision parameter (). The sensory state of the integrator node applies a deterministic scaling to the lower-level state, with a weight (). Similarly, the active state deterministically scales the integrator state using the same weight (), both parameterized with a Dirac delta function shifted by .
Note that in this parametrization, states are not intended to correspond to individual neurons but rather to larger brain regions (e.g., cortical columns or larger functional coarse-grainings), where the internal mechanisms can follow complex, nested processes. The resulting computation is encoded in the prior bias and precision of the region’s internal state, leading to stochastic population activity that is communicated to other regions. This concept of coarse-graining single-neuron activity in modeling (e.g., through statistical mechanics) is a common approach in large-scale computational modeling frameworks.
We assume that the lower-level states are continuous Bernoulli states (also known as truncated exponential), denoted by . Here, , and represents an a priori bias (or level of prior evidence) in (Figure 2). The parameter functions similarly to log-odds evidence and is given by , where λ is the prior probability . See Supplementary Information 1 for details.
This probability is defined up to a normalization constant, . See Supplementary Information 2 for details. While this form of the continuous Bernoulli is not commonly used, it can be considered as a mean-field approximation of the mean output of a large number of single, discrete Bernoulli (binary) neurons.
For reasons that will become clear later, we model the prior of the integrator states as Gaussian: , where is the precision parameter. As we will demonstrate, the mean parameter of these states can be conceptualized as representing the weighted sum of the cumulative log-odds evidence for , while the precision β represents the level of confidence in this evidence. For simplicity, we set the prior mean to zero, .
The corresponding probability density function (PDF) is given by:
Next, we define the conditional probabilities of the sensory and active states, given the lower-level and integrator states, respectively: and , where is the Dirac delta function and is a weight matrix. The elements correspond to the strength of association between the lower-level nodes and the sensory nodes (see Supplementary Information 3).
Expressed as PDFs:
To complete the loop, we define the conditional probabilities of the lower-level and integrator states, given their corresponding sensory states. We assume that both the mean of the Gaussian integrators and the bias of the lower-level Bernoulli nodes will be shifted by their respective sensory inputs, and . Specifically, they are distributed as and . Their probability density functions (PDFs) are given by:
From Individual Components to Hierarchy¶
Next, we derive the joint distribution of the lower-level nodes and the integrator nodes, constructing a system comprised of multiple nodes of both types. We begin by expressing the conditional probability of the lower-level nodes, given the integrator nodes:
Given that , and using equations (2) and (7), we can express the joint distribution as follows:
It is important to note that expressing the joint distribution from the perspective of the integrator node, , yields the same result. For further details, refer to Supplementary Information 5.
Next, we observe that the states and are the ‘blanket states’ of the system, forming a Markov blanket Hipólito et al., 2021:
This Markov blanket not only separates and , but also:
From eq.-s (9) and (10), we have:
For all such that and . This implies that the joint probability for all and nodes can be written as the product of the individual joint probabilities (Figure 1C), , which results in:
Thus, it turns out that the model presented here is a special case of a more general class of powerful energy-based models known as Restricted Boltzmann Machines (RBMs, see Figure 1D), first proposed by Smolensky Rumelhart & McClelland (1986). For similar notions, see Barra et al. (2012)Mehta et al. (2019)Kaplan et al. (2018). An RBM is a bipartite energy-based model with two layers of nodes: nodes within the same layer are not connected, while nodes in different layers are fully connected. RBMs are characterized by the Gibbs/Boltzmann distribution:
The RBM energy function has the general form:
where and are functions that can be chosen freely for RBMs. In our case, , , and .
From Hierarchy to Attractors¶
We have demonstrated, using an example parametrization, that free-energy minimizing neural units (regions) can be organized into a two-layer hierarchical system (a bipartite graph). In this system, the lower-level nodes are continuously monitored and supervised by the higher-level nodes, and vice versa. We further formalized that this resulting system is equivalent to a restricted Boltzmann machine. Next, building on the work of Barra et al. (2012), Mehta et al. (2019), Smart & Zilman (2021) and others, we show that the constructed two-layer bipartite system can be transformed into an equivalent single-layer recurrent neural network. Specifically, this is a stochastic, continuous-state Hopfield network, which is composed solely of the lower-level nodes, with the integrator nodes becoming attractor states of the system (Figure 1F).
To achieve this transformation, we need to marginalize equation (12) over the integrator nodes :
This represents the joint distribution of the nodes in a Hopfield network with an energy function:
where the weight matrix (Jacobian) is defined as:
This formulation is similar to the Hebbian learning rule but involves non-binary orthogonal patterns.
The marginalization process is presented in detail in Supplementary Information 6 and takes use of the fact that the cumulant generating function for a Gaussian distribution (the distribution of the integrator state) is zero for each cumulant, except and , which are the mean and variance of the Gaussian distribution, respectively. Since the Gaussian distribution is the only distribution having zero higher-order cumulants Marcinkiewicz, 1939, the marginalized attractor network will exhibit higher-order interactions for any other distribution over the integrator nodes (e.g., ). A recent example of such cases is the modern Hopfield network, also known as the associative memory network, introduced by Krotov & Hopfield (2016) and Demircigil et al. (2017)
Global Active Inference in the Attractor Network¶
Free energy, in the thermodynamic sense, is well understood in attractor networks. According to Amit (1989), in stochastic Hopfield networks, “the free energy is a natural extension of the energy landscape description to situations with noise.” In the thermodynamic sense, free energy is defined as , where represents internal energy and corresponds to the network’s energy function, denotes entropy, and is the temperature, so that , where Z is the partition function.
We write up free energy from the point of view of a single (lower-level) node of the attractor network, , given observations from all other nodes, :
Where is the approximate posterior distribution over , which we will parametrize as a with variational bias . simply denotes all other states. F can be expressed in two other, equivalent ways:
Intuitively, the last equation tells us that minimizing free energy will lead to a (local) minimum of the energy of the attractor network (accuracy term), with the constraint that this has to lie close to the initial state (complexity term).
From eq. (15):
The expected value of the is a sigmoid function of the bias, (Supplementary Information 4). For simplicity, we will denote it as .
The complexity term in eq. (20) is simply the KL-divergence term between two distributions:
For details on the derivation, see todo:SI.
The accuracy-term in eq. (20) can be expressed as:
Leading to the following expression for the free energy:
where C denotes all constants in the equation that are independent of σ.
For details on the derivation, see todo:SI.
Now, taking the partial derivative of the free energy with respect to the variational bias:
Setting the derivative to zero and solving for , we get:
Substituting this back into the expression for :
which is the update rule for the continuous-state stochastic Hopfield network.
Consequences¶
Attractors, Bayesian Causal Inference, and Predictive Coding¶
The nervous system cannot simply combine all signals into a joint estimate; it must infer which signals share a common cause and only integrate those. Bayesian Causal Inference (BCI) has been proposed as a unifying theory for how the brain infers causal structure from observational data Shams & Beierholm, 2022. For instance, it helps determine whether multisensory cues originate from a single source or multiple sources Körding et al., 2007. Integrator nodes in the RBM-like architecture, and equivalently, attractor states in the Hopfield-like attractor network, can be naturally interpreted as implementing BCI. To illustrate this, consider a simple network with two lower-level nodes corresponding to two distinct features, and (representing evidence e.g. for an auditory and a visual event, respectively), and a single integrator attractor μ that models the causality between these features. Here, provides evidence for a causal relationship. For simplicity, the precision of the integrator node is set to 1.
In this scenario, equation (12) reduces to:
Next, due to (11):
In other words, the auditory posterior distribution of depends on the prior bias of the visual node through the strength of the causal relationship between the two features, as determined by the posterior of the integrator node μ. The stronger the causal relationship, the greater the influence of on . Conversely, if there is no causal relationship, the auditory posterior will be independent of the visual prior. This behavior, illustrated in Figure 3, is analogous to Bayesian Causal Inference (BCI) as formalized by Körding et al., 2007. It demonstrates how attractor dynamics can implement a generalized form of Bayesian causal inference (with an arbitrarily high number of features and casual structures to infer). This is depicted in the figure below (Figure 3).
It is helpful to demonstrate how the expected value of the posterior distribution of the auditory state , given the visual state , depends on the prior biases in both states. To achieve this, we utilize the fact that follows a Gaussian distribution with a mean of and a variance of (see Supplementary Information 4):
Since the expected value of the restricted distribution is a sigmoid function of its parameter (refer to Supplementary Information 5):
By setting , we obtain:
In the case of contradictory evidence where , this simplifies to:
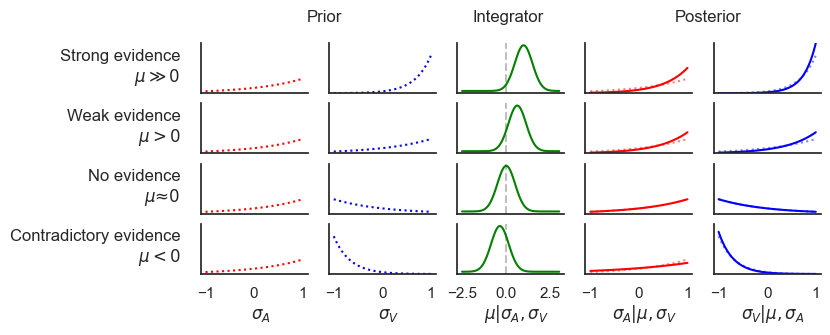
Figure 3:Bayesian Causal Inference implemented in the proposed framework.
The figure illustrates the prior (first two columns) and posterior (last two columns) distributions of the auditory state (red) and visual state (blue) under various levels of prior biases, which represent the outcome of bottom-up sensory processing. The four rows correspond to four scenarios: (1) strong evidence for a common cause (, ), (2) weaker evidence for a common cause (, ), (3) inconclusive evidence suggesting no causal relationship (, ), and (4) strong visual evidence contradicting the auditory signal (, ).
The posterior of the integrator state (middle column, green) infers the causal relationship between the two events. If the integrator node is not activated, the two events are considered independent. If the integrator node is activated, the network infers that the two events are caused by the same source. Consequently, through active inference, the visual node’s posterior will depend on the auditory node’s prior (and vice versa). The strength of this dependency is determined by the level of evidence for a causal relationship. In the posterior distribution plots, dotted lines denote the corresponding prior distribution for comparison.
In an attractor network with multiple attractors, the causal structure corresponding to the -th attractor is represented by th RBM-weights and and distributed across . For this figure, the auditory and visual weights are both set to 1 for simplicity. The precision of the integrator node β affects the strength of active inference by μ on and , i.e., the strength of the feedback effect from causal inference.
See Supplementary Information 7 for analysis code.
Alternatively, by modifying (i.e., introducing a top-down inhibitory connection) and setting and in equation (31), the system implements predictive coding. To distingush this case from the previous one, we rename teh subscripts and to (predicted) and (observed), respectively. In this case, we can write:
Here, can be interpreted as a prediction, represents a prediction error signal, and corresponds to the learning rate. This encapsulates the core concept of predictive coding, where the integrator node μ calculates and signals a prediction error towards both and . Further details and demonstrations can be found in Supplementary Information 8.
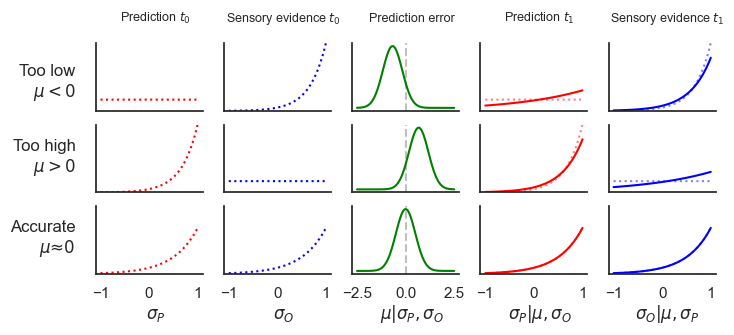
Figure 4:Predictive coding implemented in the proposed framework.
By introducing inhibitory connections, our framework can implement predictive coding. The left two columns in the figure display the probability density functions (PDFs) of the initial states, representing predicted (, red dashed line) and observed (, blue dashed line) sensory evidence. The integrator node μ (middle column, green) signals the prediction error, which is then used to update both the prediction and the sensory evidence (right two columns, red and blue solid lines, respectively).
The three rows illustrate three scenarios: (1) the predicted level of evidence is too low compared to the observations (, ), (2) the prediction is too high (, ), and (3) the prediction aligns with the sensory evidence (, ).
The strength of the prediction error feedback is determined by the precision of the integrator node β. Based on the prediction error signal, both and are updated according to the principles of active predictive coding. For the presented analysis, we set (for a more pronounced effect), , and . See Supplementary Information 8 for analysis code.
Reconstruction of Attractor States from Activation Timeseries of Lower-Level Nodes¶
So far, we have shown that high-level information integration, Bayesian causal inference, and predictive coding does not have to be performed in dedicated top-level brain hubs, but can all be implemented by the attractor dynamics in the network. But how can we identify the attractor states in the network? Here, we propose an analytic and a computational approach to reconstruct large-scale attractor states from the activation timeseries of the lower-level nodes. We start from the fact that, with the chosen parametrization, the weights of the attractor network can be approximated from the inverse covariance matrix of the activation timeseries of the lower-level nodes. Specifically, the weight matrix of the attractor network can be reconstructed as the negative inverse covariance matrix of the activation timeseries of these lower-level nodes:
where is the covariance matrix of the activation timeseries of the lower-level nodes, and is the precision matrix. For a detailed proof, refer to Supplementary Information 9.
Having estimates of the weight matrix of the attractor network, we propose two methods to identify the weights of the corresponding RBM-like network, and thus the attractor states responsible for large-scale information integration.
Analytical approach: eigenvector decomposition of the Jacobian matrix¶
With certain assumptions, the attractor states, i.e. the RBM-weights of the network can also be reconstructed analytically. Specifically, we have to assume that the brain is (close to) a projection network Personnaz et al., 1985, which is a form of Hopfield networks that provides highly stable attractors and increased storage capacity by orthogonalizing the patterns to be stored. According to Kanter & Sompolinsky (1987) This gives a unique solution for the weight matrix of the network. In the thermodynamic limit, the embedded patterns are eigenvectors of the Jacobian matrix with an eigenvalue and configurations which are orthogonal to them are eigenvectors with an eigenvalue of .
Thus, if the number of regions considered is sufficiently large, we can approximate the attractors of such a system with the eigenvector decomposition of the Jacobian matrix of the Hopfield network:
where represents the eigenvectors and denotes the eigenvalues of the matrix .
The attractor states are then given by:
where is the -th component of the -th eigenvector, and is the -th eigenvalue of the matrix . For the detailed mathematical derivation, see Supplementary Information 10 and Kanter & Sompolinsky, 1987.
It is important to note that this approach is closely related to Principal Component Analysis (PCA). In PCA, the eigenvector decomposition of the covariance matrix is fundamental, with the eigenvectors representing the principal components and the eigenvalues indicating the variance explained by each component. The connection between large-scale attractors and PCA may explain the success of studies employing PCA and related decomposition techniques on fMRI timeseries Viviani et al., 2004Di & Biswal, 2022 and elucidate the mechanisms by which such components may implement large scale information integration. Another notable connection to existing methodologies is that the attractor with the highest eigenvalue, as determined through the analytical approach, corresponds to the eigenvalue centrality of each node. This special attractor state may play a key role in broadcasting information to other nodes and maintaining homeostatic dynamics. Although eigencentrality mapping has become a widely used and effective technique Lohmann et al., 2010Binnewijzend et al., 2013, our work elucidates the computational principles underlying this method.
Computational approach: functional connectivity-based Hopfield Network¶
The computational approach to reconstructing the attractors of the system starts with constructing a stochastic continuous-state Hopfield network from and use it as a generative computational model for large-scale brain dynamics, as previously proposed in Englert et al., 2023. The attractor states of the network can be identified by repeatedly relaxing the network with random initial conditions (as previously done in Englert et al. (2023)).
Comparing the analytical and computational approaches¶
If our assumption about the brain operating as a projection network holds, the analytical and computational approaches should yield the same results, at least in an ideal scenario of no measurement noise. However, current in-vivo measurement techniques like fMRI, FNIRS, EEG, and MEG provide notoriously noisy and biased estimates of neural timeseries. Nonetheless, we could expect that at least the most stable attractor states should remain similar to those obtained analytically.
We have tested this hypothesis by comparing the attractor states obtained analytically and computationally from resting state fMRI data of n=47 healthy volunteers (see Methods for details, for analysis source code and for replication results in an independent dataset). To maximize signal to noise, we based the reconstruction on the population level negative inverse covariance matrix (as in Englert et al., 2023). This approach is only beneficial in case of attractor states that exhibit a low between-participant variability.
We found a good correspondence between the analytical and computational approaches for the first X attractors, providing initial evidence for (i) the plausibility of our assumption about the brain operating as a projection network and (ii) indicating that these attractors have a relatively low between-participant variability in the samples we used (n=47 and replicated in n=40).
Furthermore, the results provide evidence for the neuroscientific relevance of the attractor states. The spatial patterns of the obtained attractor states exhibit high neuroscientific relevance and closely resemble previously described large-scale brain systems. The first 6 analytically reconstructed attractors are shown in Figure 5A. We reconstructed the energy landscape over the first 6 attractors by constructing a t-SNE embedding on the weights of these attractors, transforming empirical resting state fMRI data of n=42 participants (xxxx time-frames) onto this embedding and computing the energy of each time-frame based on eq. (16). Results are presented on Figure 5B-F). The spatial patterns of the obtained attractor states exhibit high neuroscientific relevance and closely resemble previously described large-scale brain systems. The first attractor implements a weak but widespread coupling across the whole brain, indicating a central integrative state, possibly implementing a broadcasting effect to facilitate exchange across more distant attractors. The second attractor seems to represent two complementary brain systems, that have been previously found in anatomical, functional, developmental, and evolutionary hierarchies, as well as gene expression, metabolism, and blood flow, (see Sydnor et al. (2021) for a review), an reported under various names, like intrinsic and extrinsic systems Golland et al., 2008, Visual-Sensorimotor-Auditory and Parieto-Temporo-Frontal “rings” Cioli et al., 2014, “primary” brain states Chen et al., 2018, unimodal-to-transmodal principal gradient Margulies et al., 2016Huntenburg et al., 2018 or sensorimotor-association axis Sydnor et al., 2021. A common interpretation of these two patterns is that they represent (i) an “extrinsic” system linked to the immediate sensory environment and (ii) an “intrinsic” system for higher-level internal context, commonly referred to as the default mode network Raichle et al., 2001. The third attractor resembles to patterns commonly associated with perception–action cycles Fuster, 2004, and described as a gradient across sensory-motor modalities Huntenburg et al., 2018, recruiting regions associated with active engagement (e.g. motor cortices) and passive perceptual inference (e.g. visual areas). Somewhat more speculatively, attractors 4, 5, and 6 appear to resemble patterns that are commonly associated with executive-emotional, procedural-adaptive, and focused-distributed attentional spectra, respectively. Higher order attractors tend to become more and more sparse (fewer regions with higher weights), which may suggest they infer increasingly specific causal relations.
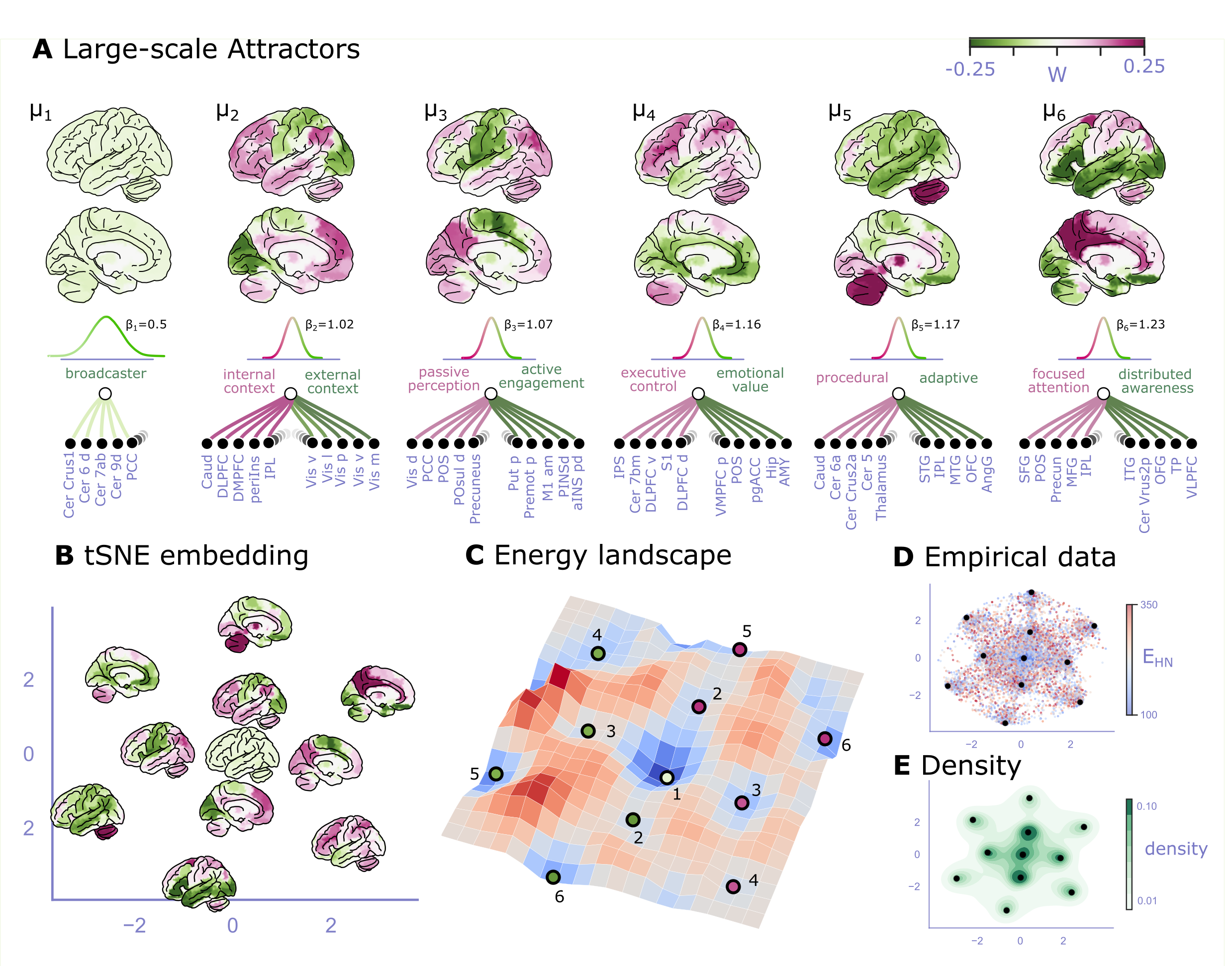
Figure 5:Large-scale Brain Attractors Reconstructed from fMRI Activation Timeseries.
This figure shows the first 6 large-scale attractor states derived analytically from the activation timeseries of “lower-level” nodes, as measured with resting state fMRI on n=46 healthy volunteers. The reconstructed attractor states are in good correspondence with those obtained with the computational approach, termed as functional connectivity based Hopfield Neural Network (fcHNN) modelling in Englert et al., 2023. This correspondence is shown in Supplementary Analysis 1.
A Attractor states are visualized by the weights they would have to the lower-level nodes in an RBM-like hierarchical architecture. Weights are shown on surface plots (left hemisphere). The eigenvalue corresponding to the attractor can be interpreted as the precision of the integrator node β. The top 5 positive and negative weights and the corresponding brain regions are displayed at the bottom of the panel as small graphs.
Based on the spatial patterns of attractor weights, somewhat speculatively, we can assign functions to the attractor states. The first attractor displays a weak but widespread coupling across the brain, suggesting a role in facilitating communication between distant attractors (i.e. how much information is broadcasted to all other regions).
The second attractor strongly resembles two complementary brain systems, often referred to as intrinsic and extrinsic systems. The intrinsic system is linked to higher-level internal context (e.g. default mode network), while the extrinsic system is connected to the immediate sensory environment.
The third attractor is likely associated with perception–action cycles, involving regions related to active engagement (e.g., motor cortices) and passive perceptual inference (e.g., visual areas).
Even more speculatively, attractors 4, 5, and 6 appear to correspond to executive-emotional, procedural-adaptive, and focused-distributed attentional spectra, respectively. In general, higher order attractors tend to become more sparse, and may integrate increasingly specific causal relations.
B T-Distributed Stochastic Neighbor Embedding (tSNE) of the first 6 attractors and their inverse states. While the analytical reconstruction is sign-invariant (the eigenvectors are orthogonal), from the point-of-view of system dynamics, the attractors are better visualized together with their inverse-pairs. These emerge as two separate attractors in the computational approach.
C Three-dimensional visualization of the energy landscape spanned by these attractors over the t-SNE manifold. Dots indicate the attractor states shown on A and B. Purple or green colored dots with the same label show an attractor and its inverse pair. The color of the dot indicates which weights are considered positive from panel A. The energy landscape was generated by first projecting empirical fMRI data onto embedding shown on panel B (panel D: all timeframes, panel E: density), calculating the energy of each time-frame based on eq. (16) (color coded on panel D) and interpolating the energy values across the latent space. Results on A-F were replicated in an independent dataset (n=38), see Analysis Code: Replication Analysis.
Detailed methodology and analysis can be found in .
Attractor-timeseries as an Emergent Level of Brain Function¶
An important implication of the proposed framework, which posits that attractor dynamics are responsible for high-level integrative computations in the brain, is that these computations can be viewed as an emergent “macroscopic” description of the system. This macroscopic level is distinct from the “micro-states” due to a concept known as “computational closure.” This has recently been demonstrated in the context of Hopfield networks by Rosas et al., 2024. To illustrate this, we consider a macroscopic description of the system based on attractors rather than lower-level units. Specifically, we examine the projection of the current neural activity σ onto the j-th attractor pattern , which is represented by the dot product between them:
It is important to note that if , if , and (in the case of many lower-level nodes) if and are uncorrelated.
When measuring timeseries of neural activation in each region (e.g., with functional MRI), we can derive the attractor-timeseries:
Rosas et al. (2024) demonstrates that , where denotes Shannon entropy, indicating that is both informationally and computationally closed with respect to σ. In other words, attractor networks perform integrative calculations based on the similarity between the present and the “stored” patterns at an emergent macroscopic level, allowing information processing to occur independently of the microscopic level. This insight enables us to construct a test to determine whether a computation related to a specific behavioral or cognitive function is implemented in the attractor space. Since such functioning should be causally closed with respect to the lower-level neural activity, attractor timeseries should exhibit the same predictive capacity towards the corresponding behavioral readouts as the timeseries of the lower-level neural activity (i.e., whole brain data), when lower-level “confounds” (such as reaction times) are neglected.
To demonstrate the capacity of attractor timeseries to capture high-level information integration during tasks, we saved the attractors reconstructed from resting state fMRI data of n=46 healthy volunteers (as shown in Figure 5) and obtained their timeseries during a heat-pain task from an independent study (n=28). These were then fed into participant-level linear models, which modelled non-painful and painful trials, reported heat or pain intensity as parametric modulators, and the rating phase. We obtained the attractors with the highest association to (A) heat stimuli (regardless of whether they were painful or not), (B) perceived heat intensity, (C) pain (as compared to heat), (D) perceived pain intensity and (E) the rating phase of the experiment. Results are shown in Figure 6. We found that attractor showed the strongest association with the expected BOLD-response to the heat stimulation blocks, regardless of them being painful or not (mean first-level beta: 1.19 and 1.27, p=0.0001 and 0.0003, W=54 and 31, respectively for painful and non-painful conditions). A higher-order attractor’s () activation timecourse was found to co-vary with perceived heat intensity (mean beta=5.32, p=0.003, W=77), dominated stark weight contrast between anterior (negative) and posterior (positive) supplementary motor cortices, anterior (negative) and posterior (positive) insulae, medial (positive) and lateral (negative) motor cortices, and the left (negative) and right (positive) middle temporal gyri. Pain intensity was best captured by (mean beta=0.36, p=0.008, W=88), dominated by contrasts between the cerebellar crus 1 (positive) and 2 (negative), anterior (positive) and posterior (negative) insulae, and also driven by ventrolateral somatomotor and posterior cingular activity. Pain was found to be best differentiated by attractor (mean beta=0.36, p=0.008, W=88), with dominant positive weights in the anteriodorsal and middle cingular cortices, VLPFC, contrast between anterior (negative) and posterior (positive)DLPFC and negative contribution among others from primary visual cortex. Attractor was found to be most active during the rating phase, characterized by positive weights in lobule 9 of the cerebellum, ventral caudatum, dorsal part of VLPFC, hippocampus and amygdala. The orbitofrontal areas, ventral thalamus and posterior putamen contributed with negative weights.
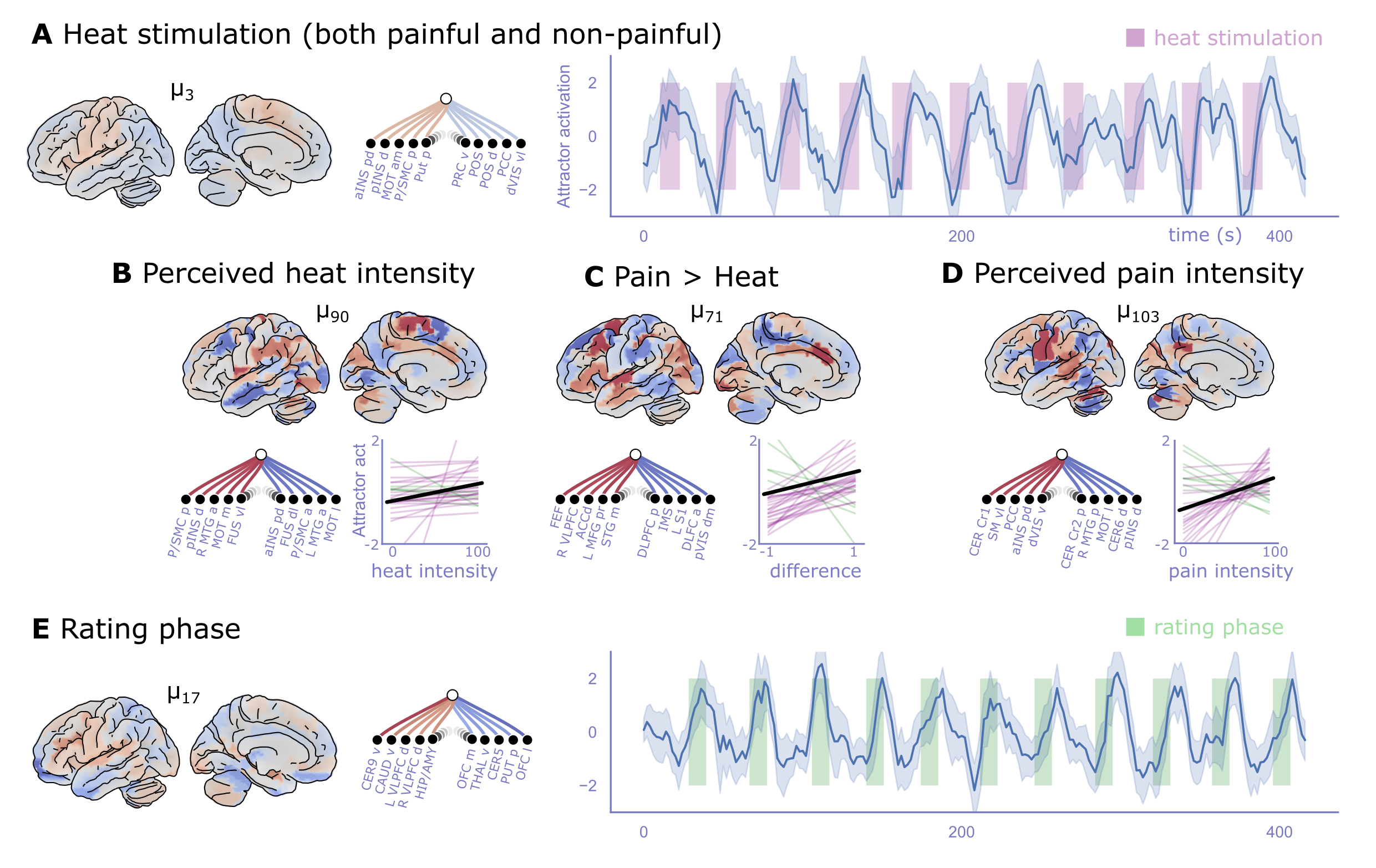
Figure 6:Information Integration by Large-scale Brain Attractors During Tasks.
The attractor states reconstructed analitically from resting state fMRI data of n=46 healthy volunteers (Figure 5) were used to generate timeseries of attractor activations (e.q (38)) throughout an independent task-based fMRI study in n=28 healthy volunteers.
A Attractor showed the strongest association with the expected BOLD-response to the heat stimulation blocks, regardless of them being painful or not (mean first-level beta: 1.19 and 1.27, p=0.0001 and 0.0003, W=54 and 31, respectively for painful and non-painful conditions). This attractor is characterized by positive weights to the insula, primary, pre-, and supplementary motor cortices, as well as to primary somatosensory areas, and negative weights to visual, posterior cingular regions, among others.
The graph plots on this and all other panels show the top five regions with the strongest negative and positive weights to the given attractor. The timeseries plot shows the mean and bootstrapped 95% confidence intervals of the attractor responses across the n=28 participants. Shaded purple areas show the heat stimulation blocks.
B Concentrating on non-painful trials exclusively, attractor 's activation timecourse showed a tendency to co-vary with perceived heat intensity (mean first-level beta=5.32, p=0.003, W=77). Regression lines for each participant (red: positive, green: negative) and the mean regression line (black) are displayed to illustrate the effect size. Interestingly, the same attractor was negatively activated in pain trials (mean beta=-0.30, p=0.032, W=109). This attractor is characterized by a strong weight contrast between anterior (negative) vs. posterior (positive) supplementary motor cortices, anterior (negative) vs. posterior (positive) insulae, medial (positive) vs. lateral (negative) motor cortices, and the left (negative) vs. right (positive) middle temporal gyri.
C Attractor 's activity was significantly higher for painful than for non-painful; trials (mean beta=0.36, p=0.008, W=88). This attractor is dominated by weight contrasts between the cerebellar crus 1 (positive) vs. 2 (negative), anterior (positive) vs. posterior (negative) insulae, and also driven by ventrolateral somatomotor and posterior cingular activity.
D Perceived pain intensity was most significantly associated with the activation of attractor (mean beta=2.93, p=0.009, W=81). The association of this attractor to painful trials, regardless of the intensity of pain, was: mean beta=0.49, p=0.001, W=53. The attractor is characterized by positive weights in the anteriodorsal and middle cingular cortices, VLPFC, contrast between anterior (negative) and posterior (positive)DLPFC and negative contribution among others from primary visual cortex.
E Attractor was found to be most strongly activated during the rating phase (mean beta=1.18, p=0.000003, W=21). The same attractor was negatively associated with pain (mean beta=-0.54, p=0.012, W=85). It is characterized by positive weights to lobule 9 of the cerebellum, ventral caudatum, dorsal part of VLPFC, hippocampus and amygdala. The orbitofrontal areas, ventral thalamus and posterior putamen contributed with negative weights.
Shaded green areas on the timeseries plot show the rating blocks.
Analysis source code is available in Analysis Code: Attractors during task.
Discussion¶
This study presents a new framework that challenges traditional hierarchical models of brain organization. Rather than attributing high-level information processing to specific hub regions, this framework suggests that such functioning is, at least in part, implemented by large-scale attractor dynamics, arising from the interconnected network of neural units. This perspective provides a plausible and compelling explanation for how the brain integrates information across multiple scales to produce coherent experiences and behaviors. Below, we discuss how the notion that large-scale attractors perform higher-order integrative computations in the brain is supported by evidence in the literature and the empirical results presented in the present work. We will, furthermore, discuss the the assumptions and requirements of applying this concept on empirical data, with focus on fMRI. Finally, er discuss implications, applications and limitations of the presented framework and conclude with testable predictions to motivate further research.
Plausibility and Initial Evidence for the Significance of Large-Scale Attractor Dynamics in the Brain¶
Though largely theoretical, our framework finds support in existing research on brain network organization and dynamics. Attractors have long been proposed to play a crucial role in the brain’s information processing at the circuit-level. They are believed to underlie a wide range of cognitive functions, including memory, sequence generation, integration, and robust classification and decision-making Freeman, 1987Amit, 1989Deco & Rolls, 2003 Tsodyks (1999). The level of evidence is somewhat lower at the macro-level. While computational work has convincingly shown that multi- and metastable attractor dynamics do extend to the meso- and macro-scales Rolls, 2009Kelso, 2012Haken, 1978Breakspear, 2017Deco & Jirsa, 2012Kelso, 2012, the phenomenon of attractor dynamics on the macro-scale, and especially, their relation to cognition and behavior, are much less understood, as compared to the circuit-level. Multiple studies suggest, however, that the brain’s near scale-free topology makes it particularly amenable to the emergence of large-scale attractor dynamics. Furthermore, there is robust empirical evidence that large-scale brain dynamics align with the most common formalization of the update rule for attractor networks: brain activity in a held-out region can be accurately predicted as the weighted sum of the activity in all other regions, with the weights being the functional connectome Cole et al., 2016Sanchez-Romero et al., 2023Cole, 2024. In a recent analyses, we took use of this analogy and constructed attractor networks with weights initialized based on this “activity flow” and found that these networks exhibit attractor dynamics with high stability, fast convergence and neuroscientific relevance Englert et al., 2023. Using these networks as a large-scale phenomenological model of neural dynamics accurately predicted a variety of brain dynamics, from task-states to disease conditions.
From a evolutionary point-of view, an attractor-based system for large-scale information integration presents several advantages, both in terms of fault tolerance and efficiency. Fault tolerance in attractor networks is boosted by eliminating single-points-of-failure at two levels. First, there is no physical integrator node to be damaged. Second, the weights of integration, which can be considered the “software code” for high-level inference, are well protected as they are distributed across multiple connections (). Advantages in terms of efficiency stem from the staggering memory capacity of attractor networks. Even with basic formulations, like the herein presented stochastic continuous Hopfield-architecture, the capacity of the attractor network can reach the theoretical bound where the number of attractors equals the number of nodes Fachechi et al., 2019, when efficient learning and unlearning techniques are applied. In this case, attractor networks require around half the connections () compared to explicit top-level integrator nodes () (see Figure 7A). It is possible, however, that this capacity limit is significantly higher. With non-Gaussian integrator nodes, higher-order interactions will begin to influence the network’s dynamics, substantially increasing the “memory capacity” of these networks. An example of networks with higher-order interactions is modern Hopfield networks (also known as Dense Associative Memories), which have recently been recognized as a major advancement in artificial intelligence research Krotov & Hopfield, 2016Demircigil et al., 2017. While at first glance, the need for “many-body synapses” to implement such architectures may seem neurobiologically implausible, recent work has shown that these networks are equivalent to more biologically plausible networks using “memory neurons” Krotov & Hopfield, 2020 or neuron-astrocyte synapses Kozachkov et al., 2023. It is therefore compelling to hypothesize that the brain can exploit both advanced learning/unlearning techniques and higher-order interactions, thereby constructing a computational architecture with exponential “memory capacity.” This would mean that the maximal number of attractors is no longer a limiting factor (see Figure 7B) and would position attractor dynamics as a highly appealing mechanism to accommodate the richness of human experiences, cognitive and metacognitive abilities.
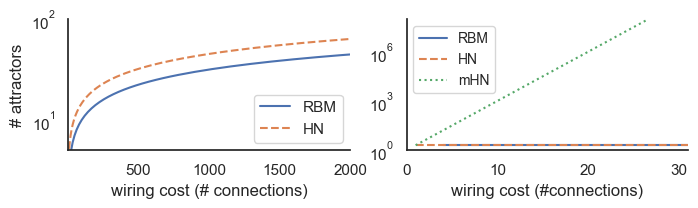
Figure 7:Information integration in the attractor domain requires fewer connections than explicit top-level integrator nodes. A The number of connections (wiring cost) required for a restricted Boltzmann Machine (RBM, blue) with the same number of integrator nodes as attractors stored by a saturated Hopfield network. B Modern Hopfield networks or Dense Associative Memory networks have exponential storage capacity. Although these networks involve higher-order interaction terms (i.e., “many-body synapses” connecting more than two units), which limits their neurobiological plausibility, they have recently been shown to be equivalent to more biologically plausible networks when extended with “memory nodes” Krotov & Hopfield, 2020. For Python code to generate the plots, see Supplementary Information 11.
Todo: discuss these too: Gosti et al. (2024) Gohil et al. (2022)
In light of all these considerations, the existence and significance of large-scale attractor dynamics seem to be beyond any doubt. The question seems to be how the functional and computational properties of attractor dynamics can be understood in terms of our existing concepts of neural computations and whether we can measure and reconstruct them empirically.
Attractor dynamics as a basis for a broad-scope computational system¶
Both at the macro- and circuit-level, intermingled recurrent connections of an attractor network can be complex to understand. The presented theoretical framework offers several important insights into the intricate nature of attractor dynamics. It substantiates that transforming the weights of an attractor network into a bipartite RBM-like graph allows for a clearer interpretation, with direct insights into the weights along which information is integrated. As a direct consequence, the framework clarifies how attractor dynamics can implement (Bayesian) causal integration or predictive coding, and that the precision of information integration, or the learning rate of the system, can be encoded within these functional connections (β in eq. (17)).
Our framework, grounded in the Free Energy Principle (FEP), allows for the treatment of lower-level computational units as “black boxes”, in a sense that the internal computations leading to biases in lower-level regions can be arbitrarily complex. Therefore, it might be of particular significance for understanding the role of attractor dynamics in large-scale brain function. Our prototypical mathematical formulation allows for both analytical and computational approaches to reconstruct attractor states from the activation timeseries of “physical” brain regions, as measured e.g. by resting state fMRI. Our initial results, as well as those presented in Englert et al. (2023), suggest that the reconstructed attractors possess a high neuroscientific relevance and, in many cases, they strongly resemble previously described brain subsystems, like the default mode network. Our framework provides a new lens through which to interpret these subsystems and equips previous descriptive techniques to discover them with an underlying mechanistic model. For instance, eigencentrality, a measure used to identify important nodes in a network Lohmann et al., 2010Binnewijzend et al., 2013, takes on new meaning when viewed through the framework of attractor states. Regions with high eigencentrality are no longer just hubs; they are key players within the brain’s strongest attractor states, suggesting that changes in their activity can have a more significant role in regulating the degree to which information is broadcasted in the brain in a given moment.
While attractor patterns represent key features of the system, the complex dynamics around these attractors might be even more important to understand. The computational approach proposed in this paper and in Englert et al. (2023) can reconstruct not only the attractors themselves but also the dynamics induced by them. Individual differences and alteration in these dynamics might be responsible for a wide variety of behavioral phenomena. For instance, depending on the energy landscape (C), switching between modes of operation (or transitioning between the basins of different attractors) might be altered in certain neurological conditions and might serve as a powerful predictor of treatment response. On the high-diemnsional attractor manifld, an attractor can be approached from multiple initial conditions, leading to system degeneracy, where different conditions result in similar experiences (e.g., acute, chronic, or emotional pain). We argue that recovering and predicting subtle but significant differences in attractor dynamics from empirical data may be one of the most promising avenues in our framework. Such approaches would hold potential to precision interventions, e.g. by means of non-invasive brain stimulation techniques, to achieve changes in the energy-landscape that alleviate symptoms of certain neurological and psychological conditions.
What makes a suitable low-level node?¶
It is important to discuss the assumptions and requirements for the proposed practical methods to reconstruct attractor states from empirical data. Activity time-courses in lower-level nodes can be measured using various techniques, including resting-state functional MRI (rs-fMRI). However, these measurements come with inherent limitations. For example, empirical functional connectivity in rs-fMRI experiments reflects slow changes (<0.1 Hz) in synchronization dynamics and mixes signals from spatially proximate regions. From a purely theoretical perspective, any arbitrary set or network of neurons can be considered as one or multiple FEP-agents, and thus our results hold for any arbitrary coarse-graining of the brain. However, it is evident that with inappropriate coarse-grainings, the resulting system will not be able to reconstruct meaningful attractors. An critical requirement of reconstructing attractor dynamics from empirical data is, therefore, the use of an appropriate coarse-graining, a.k.a brain parcellation. One strategy to constructing an appropriate coarse-graining is to lump together regions that are functionally coherent and, therefore, have a very similar effect on the strongest attractors (highest eigenvectors) of the system. Such coarse-graining is done very effectively by various functional parcellation approaches, that take use of the spatially autocorrelated nature of the brain and lump together regions with similar functional connectivity. Theoretically, the more fine-grained the parcellation, the more attractors we can reconstruct and the more accurate the reconstruction of the higher-order attractors will be. This is, however, obviously limited by the signal-to-noise of empirical data, as well as the large inter-individual differences in brain structure and function. Precision neuroimaging Gratton et al., 2022 offers a primising approach to overcome these challenges. In terms of temporal resolution, there is evidence, that the neural signal of interest, that gives rise to multistability and large-scale attractor dynamics, yield fluctuations that are substantially slower than the timescales of the single-node neural dynamics and extends into the slow timescales of the hemodynamic response Heitmann & Breakspear, 2018Medrano et al., 2024. Specifically, fast components of neuronal activity are thought to show exponential decay towards an ‘inertial manifold’ (see central manifold theory), that is, a generalised surface that is aligned with the weak directions of the flow Carr, 1981. This effectively separates brain activity into fast and slow components, that evolve on different temporal scales. Over long periods of time, the macroscopic behaviour of the system can be described by the evolution of slow variables Kuramoto & Nakao, 2019, possibly establishing an information closure between fast micro-sates and emergent slow macro-states. The slow modes (which flow on the centre manifold) are then said to enslave the fast modes (which the centre manifold attracts), often referred to as the “slaving principle”. This allows for adiabatic approximation Jafarian et al., 2021: the fast variables are replaced by their steady-state solution and, in essence, provides the rationale for assessing large-scale attractors by measuring the slow components of the neural activity, as done in fMRI.
Attractors, Markov blankets and Emergence¶
An important implication of our framework is that, as a consequence of marginalizing the the RBM-like hierarchy to a Hopfield-like attractor network, the lower level nodes themselves become a Markov blanket. From the countless Markov-blankets within the brain, this special, “top-level” blanket is a very remarkable one; it is the one that separates emergent macro-scale computations from the outer world (see Figure 8). This insight may have appealing, albeit admittedly speculative, implications for the neuroscience and philosophy of mind and consciousness. Specifically, the Markov blanket between the attractors and the lower-level nodes might be the the inner boundary (“inner screen”) described by Ramstead et al. (2023). Information encoded on this Markov blanket is obviously not an exhaustive or complete description of the system. It only stores the “most relevant” information, that is, the information that is necessary to understand the represented world at the highest level of abstraction. This means that certain underlying computations remain in the lower-level nodes, without any effect on the high-level emergent representation. In other words, certain details necessarily remain “unconscious” for the highest level of information integration in the brain. Even more speculatively, it just takes one more step to extend this theory from the scope of a single brain to multiple brains: attractors arising from inter-individual communication. The interaction of potential attractors inside and outside our heads may provide a novel framework for understanding societal and cultural phenomena, such as language, norms, beliefs and their spread and evolution in the society.
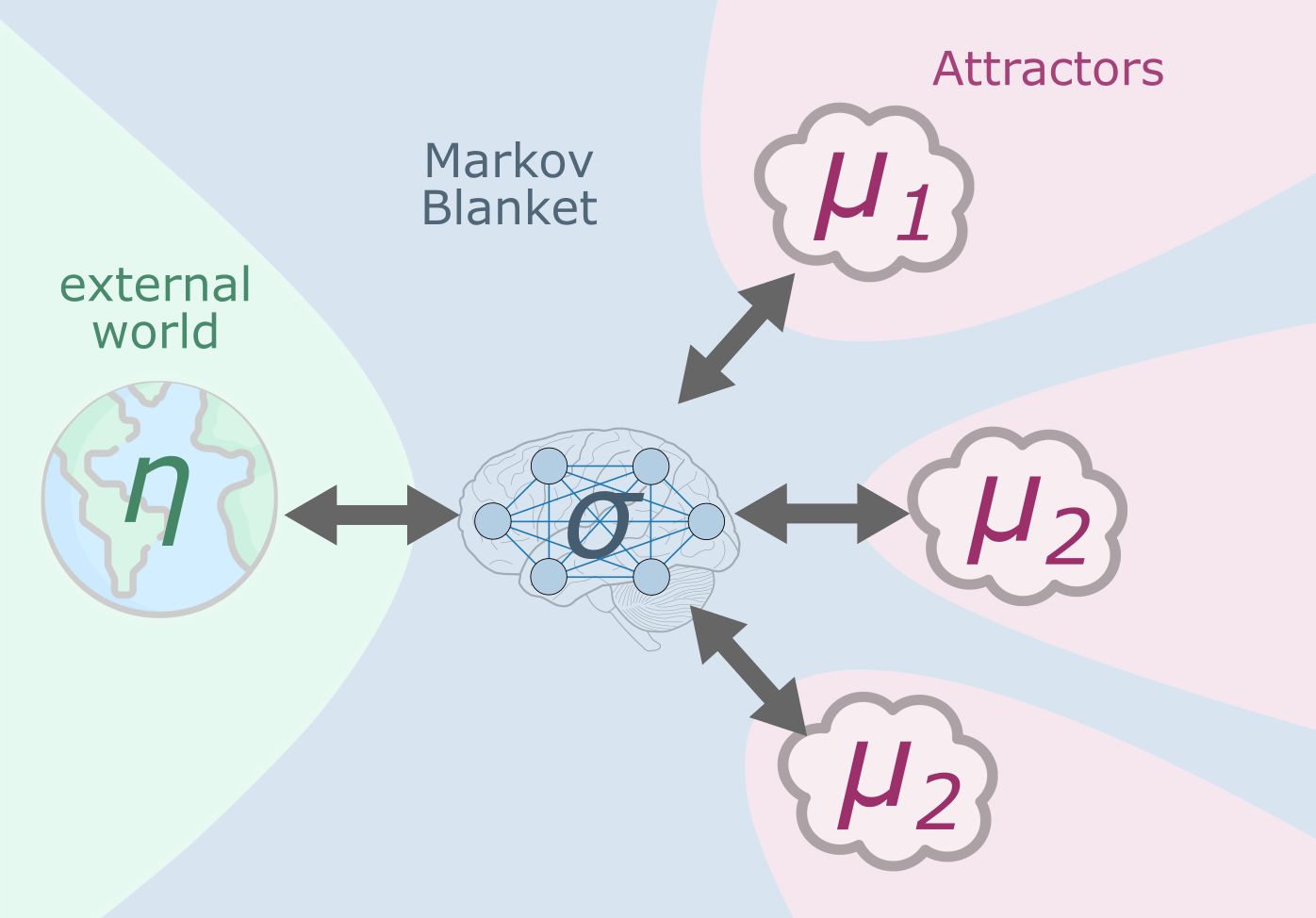
Figure 8:Attractors and Markov blankets In the proposed framework, marginalizing the the RBM to a Hopfield architecture implies that the lower level nodes themselves become a Markov blanket separating lower level computations and high level integrative function in the attractor space. The Markov blanket that separates the external world from the top-level computational attractor layer is composed by all “physical” nodes of the whole brain. Thus, in our framework, the “innermost screen”, as proposed by Ramstead et al. (2023), is the brain itself.
Limitations¶
The mathematical formalization presented here is not intended to be a comprehensive model of the brain’s large-scale attractor dynamics. Instead, the analytical and computational approaches we have introduced should be viewed as an initial step towards a deeper understanding of these dynamics. Further refinements and validations are necessary. However, we believe that many of the assumptions in our prototypical formulation, such as the symmetry assumption in equation , can likely be relaxed. Consequently, this work can serve as a foundation for developing more detailed, realistic models of the brain’s large-scale attractor dynamics.
Testable Predictions¶
The theoretical framework outlined in this study offers several testable predictions that can guide future neuroscientific investigations. A key prediction stems from the fact that attractor dynamics represent an emergent level of computations (separated by a computational closure from lower levels). This implies that, for any high-level integrative function that is implemented in the “attractor-space”, the timeseries data of a few relavant attractors should be sufficient to predict the corresponding behavior. This prediction can be easily tested in many research settings. A well suited example may be placebo analgeisa, a phenomenon that requires the integration of information from many different sources (expectations, prior experiences, conditioned cues, internal states) and can lead to significantly different behavior even if the incoming sensory information is unchanged (i.e. without much involvement at the lower-levels). Our framework predicts that the degree of behavioral analgeisa should be predicted by the “timeseries” of the few most relevant attractors as well or better than by the whole brain data. Similar hypotheses can be created for numerous other examples of high-level integrative functioning and the emergent nature (computational closure) of attractor-computations can be exploited as a test to identify these functions, likely including pain, anxiety, emotions, high-level cognitive coordination, attention-focus, consciousness, and many other processes crucial for survival. By exploring the relationship between these functions and the brain’s attractor landscape, researchers could gain deeper insights into the neural mechanisms underlying these complex processes.
todo refine other examples
A related prediction is that, in many cases, causal integration and prediction errors are encoded in the attractors. Studies combining dedicated behavioral paradigms with computational modeling can test this prediction extending the search to attractor states, next to directly observable “lower-level” regions. We hypothesize, furthermore, that higher-order attractors are more specialized and, in terms of their weight distribution, sparser than lower-order attractors. By increasing the granularity of coarse-graining (e.g., through fine-grained brain parcellations and precision neural measurements), the number of identifiable attractors increases, potentially offering insights into increasingly detailed computations. Our frameworks entails, furthermore, that the interpretability of functional brain connectivity is boosted when connectivities are transformed to the equivalent bipartite space ( to ). We hypothesize that higher order, specialized attractors employ intrinsic weight arithmetics that are often based on contrasting regions with seemingly similar functionality (see e.g. Figure 6B-D). Focusing on the attractor weights, instead of functional connectivity, allows for disentangling these computational arithmetics behind higher-order computations.
Our framework promises furthermore, to link brain connectivity and task-elicited brain activations. Task-based activity, in our notion, is a product of the same network with altered prior biases in the lower-level nodes. This is expected to result in slightly different attractors (see Supplementary Analysis X), allowing adaptive behavior in various bias-configurations and further increases the capacity of the system (see e.g. the "ghost attractor of pain, Englert et al., 2024). This can be tested empirically by changing the biases, either indirectly, by various task paradigms, or directly, by means of non-invasive brain stimulation techniques like TMS. According to our framework, these manipulations should lead to characteristic shifts in the brain’s attractor landscape and thereby, predictable changes in overall brain activity. If experimentally validated, this prediction would provide strong evidence for the dynamic and adaptable nature of attractor states in shaping brain function. Thus our framework, especially when combined with network control theory, holds potential to advance non-invasive brain stimulation-based interventions.
This leads us to predictions about the potential of our framework in clinical settings. Many neurological and psychological conditions have previously been conceptualized with abnormal attractor dynamics. For instance, in depression, attractors related to negative stimuli could have lower energy or surrounded by higher-energy peaks that makes it difficult to leave the corresponding states. By mapping these changes within our framework, researchers can gain a better understanding of the neural mechanisms underlying these conditions and potentially develop targeted precision interventions to change the attractor landscape in a preferable way.
More predictions?
Conclusion¶
In conclusion, our proposed framework offers a novel perspective on the brain’s large-scale attractor dynamics. By leveraging the principle of active inference and the statistical theory of artificial neural networks, we provide a comprehensive approach to understanding the computational mechanisms of attractor dynamics and provide recipes to reconstructing them from empirical data. Our work provides a novel framework to understanding and interpreting brain activity and connectivity and opens new avenues for conceptualizing and - potentially treating various neurological and psychological conditions.
Methods¶
In our accompanying analyses, attractor states were reconstructed using a combination of functional connectivity measures and manifold learning techniques. Specifically, we employed the following steps:
Data¶
We used three separate datasets in the presented analyses. To reconstruct attractor states, we used resting-state fMRI data from N = 48 healthy volunteers (Study 1) Analysis Code: Reconstruction of the Attractor Landscape and replicated all analyses on another dataset of N=39 healthy volunteers (Study 2) Analysis Code: Replication Analysis. Details of image acquisition are provided in Spisak et al., 2020. Briefly, the data were acquired using 3T MRI scanners, at the University Hospital Essen for the first dataset, and at the Ruhr University Bochum, for the second dataset. The study was conducted in accordance with the Declaration of Helsinki, complies with all relevant ethical regulations for work with human participants and was approved by the local or national ethics committees (Register Numbers: 4974-14, 18-8020-BO and 057617/2015/OTIG at the Ruhr University Bochum, University Hospital Essen and ETT TUKEB Hungary, respectively.) All participants gave written informed consent before testing.
To demonstrate how attractors may integrate information dynamically during tasks, we used data from Woo et al., 2015 (Study 3), consisting of nine task-based fMRI runs for each of the 33 healthy volunteers. In all runs, participants received heat pain stimulation. Each stimulus lasted 12.5 seconds, with 3-second ramp-up and 2-second ramp-down periods and 7.5 seconds at target temperature. Six levels of temperature were administered to the participants (level 1: 44.3°C; level 2: 45.3°C; level 3: 46.3°C; level 4: 47.3°C; level 5: 48.3°C; level 6: 49.3°C). Participants reported the In runs 3 and 7, participants were asked to cognitively “increase” (regulate-up) or “decrease” (regulate-down) pain intensity. In the present analyses, we used run 1 (without up- or down-regulation). After each heat stimulation trial, participants judged whether the stimulus was painful or not, followed by a judgment of pain or warmth intensity on a 100-point visual analog scale, within a 11 second-long rating block.
Preprocessing¶
All three datasets were preprocessed with our in-house built pipeline: the RPN-signature pipeline (version 0.2.6) Spisak et al., 2020. The preprocessing utilized various tools from the FSL Jenkinson et al., 2012, AFNI Cox, 1996, and ANTs Avants et al., 2011 software libraries and employed nipype Gorgolewski et al., 2011 to perform the following steps: brain extraction, boundary-based co-registration from functional to anatomical space, high precision co-registration from anatomical to standard space, motion correction, nuisance regression (24 motion regressors88 and temporal SNR-based compcor {}https://doi.org/10.1016/j.neuroimage.2007.04.042 correction with 5 components), bandpass filtering (0.08–0.008 Hz) and scrubbing of high motion time frames (framewise displacement, FD > 0.15mm). Participants with more the 50% of the volumes scrubbed, were excluded from further analyses (2, 1 and 4 participant excluded in the studies 1, 2 and 3, respectively). A functional brain atlas (data-driven parcellation derived with the BASC algorithm)45 was used with 122 non-overlapping functional regions {}https://doi.org/10.12688/mniopenres.12767.2. The atlas regions were transformed back to the individual functional space and masked to retain gray matter voxels only. Regional timeseries were obtained by averaging data within the regions for all timeframes.
The inverse covariance matrix was estimated from the regional timeseries with nilearn, using the Ledoit-Wolf estimator.
Attractor Reconstruction¶
Attractor states were reconstructed both computationally and analytically from Study 1. The analytical approach was implemented in Python, based on eq. (37). For the computational reconstruction, we used the connattractor Python package Englert et al., 2024 to initialize a continuous-state Hopfield network with the functional connectome and relaxed the network with 1000 random inputs to map out its attractor states. The correspondence between analytically and computationally reconstructed attractor states is visualized in Supplementary Analysis 1.
To visualize the high-dimensional “attractor landscape” on a low-dimensional manifold, the analytically reconstructed attractor states were fed into a t-distributed Stochastic Neighbor Embedding (t-SNE). Then we projected the individual regional timeseries data onto the t-SNE-based attractor manifold, so that each time-frame corresponds to a point on the low-dimensional manifold. The energy of each point was calculated by eq. (16), with the inverse covariance matrix of the empirical data. The energy landscape was then visualized by averaging the energy values over a 20x20 grid. For better visualization, we applied a small amount of Gaussian smoothing (sigma=0.8 grid cells). All analyses were replicated in Study 2, with the same analysis parameters, except adjusting the temperature parameter of the computational model to obtain the same number of attractors as in Study 1. See Analysis Code: Replication Analysis for details.
Information Integration During Task¶
To demonstrate the capacity of attractor timeseries to capture high-level information integration during tasks, we saved the attractors reconstructed from resting state fMRI data in study 1 (as shown in Figure 5) and obtained their timeseries during a heat-stimulation task from study 3 (n=28). Then we We convolved the block design paradigm with an SPM-style hemodynamic response function to obtain hypotheses functions for the non-painful heat, pain and rating blocks. We created parametric modulators modeling the perceived heat and pain intensity. These were fed into a participant-level linear regression model to explain attractor timeseries, independently for each attractor. Regression coefficients were tested against zero at the group-level with a Wilcoxon signed-rank test, independently for each attractor. Participant level timeseries were aggregated and plotted with the Python package seaborn, showing the bootstrapping-based 95% confidence intervals of the mean across participants.
todo: more details
[^1] A holographic screen is, by definition, a boundary in the joint system-environment state space that encodes all of the information that one system can obtain about the other; hence a holographic screen functions as a Markov blanket, in the sense that it assures conditional independence between system and environment states.
- Körding, K. P., Beierholm, U., Ma, W. J., Quartz, S., Tenenbaum, J. B., & Shams, L. (2007). Causal Inference in Multisensory Perception. PLoS ONE, 2(9), e943. 10.1371/journal.pone.0000943
- Shams, L., & Beierholm, U. (2022). Bayesian causal inference: A unifying neuroscience theory. Neuroscience & Biobehavioral Reviews, 137, 104619. 10.1016/j.neubiorev.2022.104619
- Rao, R. P. N., & Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature Neuroscience, 2(1), 79–87. 10.1038/4580
- Hohwy, J. (2013). The Predictive Mind. Oxford University Press. 10.1093/acprof:oso/9780199682737.001.0001
- Tononi, G. (1998). Consciousness and Complexity. Science, 282(5395), 1846–1851. 10.1126/science.282.5395.1846